需要の価格弾力性のグラフと計算|求め方をわかりやすく
需要の価格弾力性とは
需要の価格弾力性とは、ミクロ経済学の消費者理論で出てくる需要曲線に関連したお話です。
この需要の価格弾力性のグラフの見方、計算、求め方についてわかりやすく説明します。
需要曲線と需要の価格弾力性
需要曲線は、ある財の価格と需要の関係を表す曲線です。
価格が下がったときに、需要が増えるので需要曲線は右下がりになります。
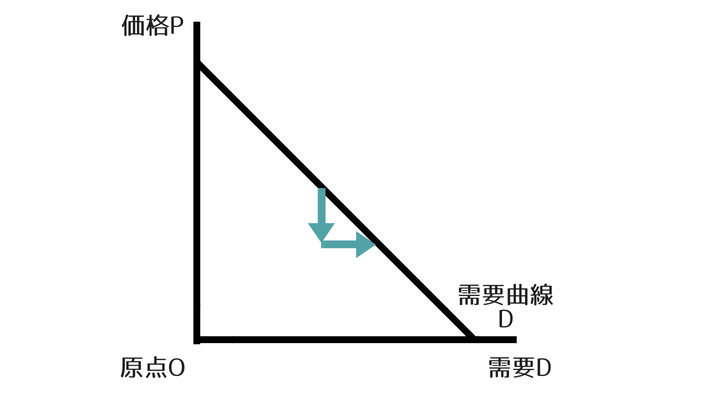
このとき価格の変化で需要がどのくらい変化するかを表す値が需要の価格弾力性のイメージです。
経済学では、この需要の価格弾力性のほかにも弾力性というものがたくさん出てきますが、その中でも需要の価格弾力性は一番重要なものになります。
そのため、経済学の勉強では、需要の価格弾力性について、求め方の式やグラフの振る舞いまでしっかり覚えておいた上で、ほかの弾力性については、「需要の価格弾力性とおんなじだね。」と理解するようにします。
需要の価格弾力性の言葉による定義
需要の価格弾力性は、価格の変化率に対する需要の変化率の大きさと定義されます。
変化率というのはどういうものかというと、たとえば、ある財の価格が100円だったときにそれが50円になったとします。
このとき価格は-50円変化したことになります。
価格P100円 → 50円のとき △P=-50
「△」の記号はデルタと読み、どれだけ変化したのかという変化分(へんかぶん)をあらわします。
このとき価格の「変化率」は100円分の-50円で-0.5つまり50%のマイナスになります。
変化率:-50円÷100円=-0.5(-50%)
一方で、このとき需要が500個から600個に増えたとすると、需要は100個変化したことになるので、需要の変化分△Dは100になります。
需要D500個 → 600個なら △D=100
ですから、変化率は500個分の100個で0.2つまり20%のプラスになります。
変化率:100個÷500個=0.2(20%)
需要の価格弾力性の数式による求め方と計算
では、このような状態で需要の価格弾力性の値を数式で計算してみます。
$$需要の価格弾力性e=-\frac{需要の変化率}{価格の変化率}$$
$$需要の価格弾力性e=-\frac{\frac{需要の変化分△D}{需要D}}{\frac{価格の変化分△P}{価格P}}$$
(分数の数式が上手く表示できないときのために割り算の式も書いておきます)
需要の価格弾力性e=-需要の変化率÷価格の変化率
需要の価格弾力性e=-(需要の変化分△D÷需要D)÷(価格の変化分△P÷価格P)
需要の変化率を価格の変化率で割ったものにマイナスをつけたものが需要の価格弾力性の求め方です。
マイナスが付く理由は、価格と需要は普通逆に動くからです。
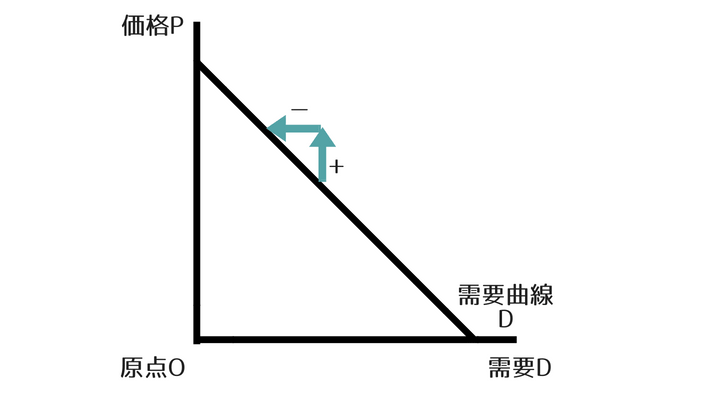
価格が高くなれば、需要は減ります。
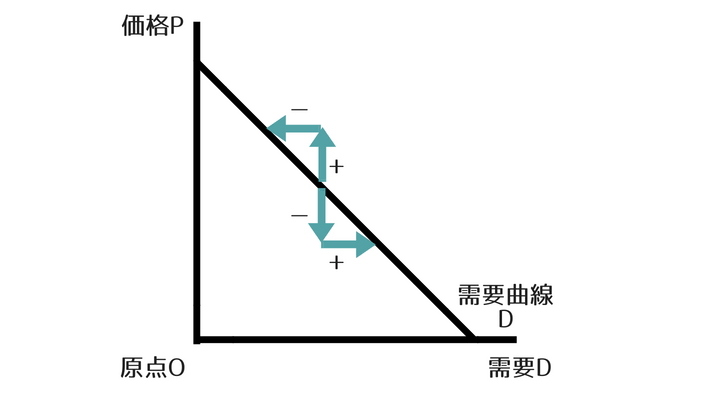
一方で、価格が安くなれば、需要は増えることになります。
とすると、価格が高くなってプラスに変化すれば、需要は減ってマイナスに変化し、価格が安くなってマイナスに変化すれば、需要は増えてプラスに変化することになります。
つまり、分母と分子のプラス・マイナスが逆になるので、単に割っただけだと、普通の場合に符号がマイナスになってしまうことになります。
そこで、普通の場合に価格弾力性がプラスになるようにするためにマイナスをつけているというのが、マイナスが付く理由になります。
さきほどの例の場合の需要の価格弾力性を計算すると、
$$需要の価格弾力性e=-\frac{0.2}{-0.5}=0.4$$
分母分子を割り算であらわすと
需要の価格弾力性e=-{0.2÷(-0.5)}=0.4
と計算できます。
価格の変化率が-0.5で、需要の変化率が0.2なので、0.2/(-0.5)にマイナスをつけて0.4が需要の価格弾力性の値になります。
簡単な計算問題ではこの例のような問題が出てきますので、例題として知っておきましょう。
需要の価格弾力性の大きさについて
次に、需要の価格弾力性の大きさについて考えます。
需要の価格弾力性が大きい財
需要の価格弾力性が大きいというのは、式でいうと(絶対値ベースで)価格の変化率よりも需要の変化率が大きいということを意味します。
これは数字(値)でいえば、1より大きいということです。
このような状態を需要は弾力的であるといいます。
こういった弾力的な財の具体例がぜいたく品です。
たとえば、海外旅行などはもともと価格が高くて需要が小さかったものが価格が安くなって需要がすごく大きく伸びるということがあります。
この場合、価格の変化よりも需要の変化の方が大きいといえるため、海外旅行などのぜいたく品は弾力的な財の例になります。
需要の価格弾力性の小さい財
次に、需要の価格弾力性が小さいというのはどういうことかというと、価格の変化率よりも需要の変化率が小さいということを意味します。
これは数字でいえば、1より小さいということになります。
このような状態を需要は非弾力的であるといいます。
そして、この非弾力的な財の具体例が生活必需品になります。
たとえば、お米などは価格が高くなっても安くなっても需要はそれほど変化しません。
したがって、お米などの生活必需品は非弾力的な財の具体例だといえることになります。
需要の価格弾力性がマイナスの財
一方で、需要の価格弾力性がマイナスのケースはどうかというと、これはギッフェン財のケースになります。
ギッフェン財とは、価格が上がれば消費量が増え、価格が下がれば消費量が減る財です。
ですから、ギッフェン財の需要曲線は通常とは異なり、右上がりになります。
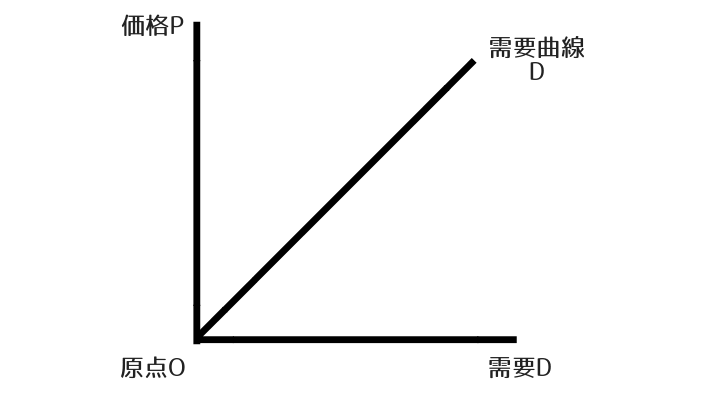
この場合、ギッフェン財は価格が上がってプラスに変化すると、需要が増えてプラスに変化し、価格が下がってマイナスに変化すると、需要が減ってマイナスに変化することになります。
そのため、ギッフェン財では価格の変化率と需要の変化率の方向が同じになります。
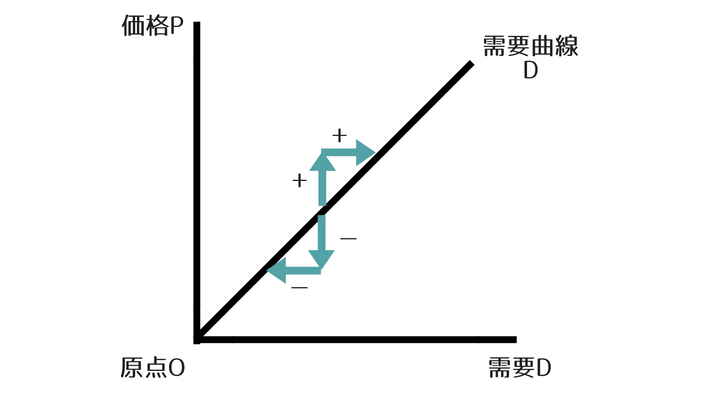
よって、需要の価格弾力性の式でいう価格の変化率分の需要の変化率の関係は、プラス分のプラスもしくはマイナス分のマイナスという組み合わせになるため、変化率同士の関係では結局プラスになることになります。
これにさらにマイナスをつけますので、ギッフェン財の需要の価格弾力性は全体としてマイナスになります。
以上が、ギッフェン財の需要の価格弾力性がマイナスになる理由です。
需要曲線のグラフと需要の価格弾力性の関係
これは需要の価格弾力性に関する需要曲線のグラフの見方についてのお話です。
需要の価格弾力性の大きさによって、需要曲線のグラフの傾きがどうなるかという点に注目します。
需要の価格弾力性が大きいケース:グラフは緩やか
需要の価格弾力性が大きい ⇒ 需要曲線は緩やかになる
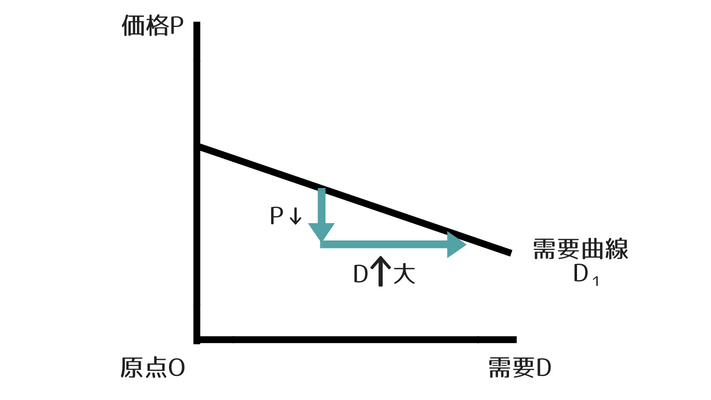
価格が下がったとき需要がどのくらい増えるかが需要の価格弾力性の大きさです。
ですから、需要の価格弾力性が大きい場合、需要曲線のグラフの傾きは緩やかになります。
需要の価格弾力性が小さいケース:グラフは急
需要の価格弾力性が小さい ⇒ 需要曲線は急になる
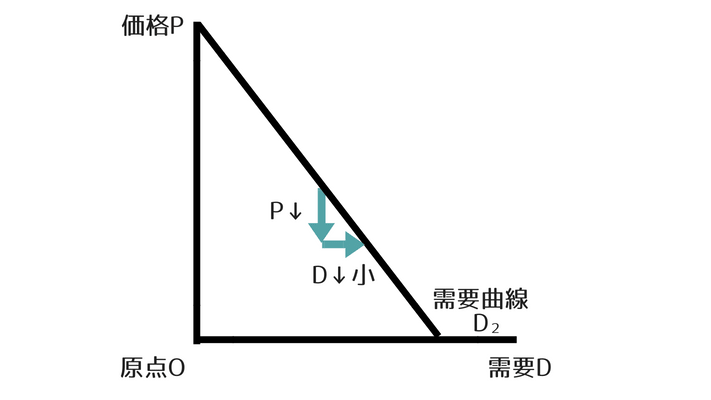
需要の価格弾力性が小さいと、価格が下がったとき需要が少ししか増えないことになります。
ですから、需要の価格弾力性が小さい場合、需要曲線のグラフは急になります。
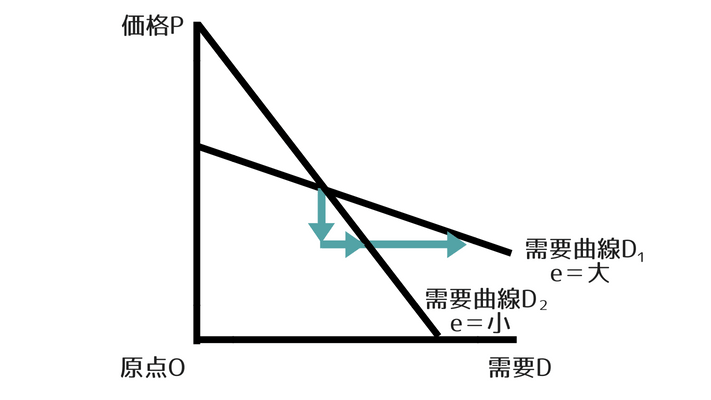
ですから、D1とD2では、D1はD2よりもグラフの傾きが緩やかなので、D1の方が需要の価格弾力性が大きいということになります。
需要の価格弾力性がマイナスのケース:グラフは右上がり
では、次に需要の価格弾力性がマイナスのケースについて考えてみます。
需要の価格弾力性がマイナス ⇒ 需要曲線は右上がりになる
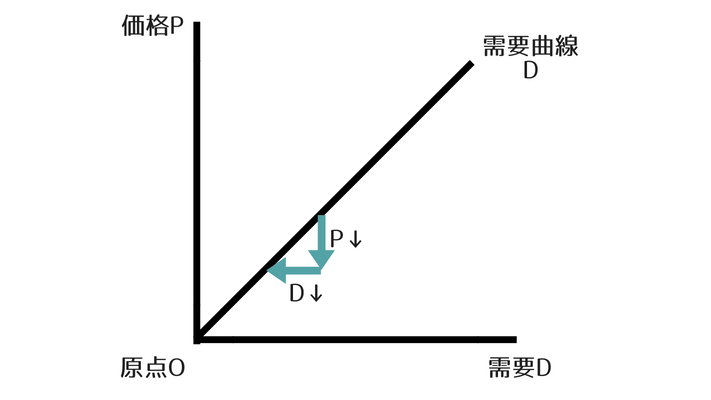
需要の価格弾力性がマイナスのケースというのは、さきほどのギッフェン財のケースです。
ギッフェン財は価格が下がると需要が減るので、需要曲線は右上がりになりました。
需要の価格弾力性が無限大のケース:グラフは水平
あと極端なケースについてもおさえておきます。
経済学では、無限大とかゼロといった極端なケースを扱うことも多いのでここでみておきます。
需要の価格弾力性が無限大 ⇒ 需要曲線は水平になる
無限大というのは、大きいのが極端になったケースです。
需要の価格弾力性が大きければ、需要曲線は緩やかになるので、極端に大きければ無限に緩やかになり、需要曲線は水平になると考えます。
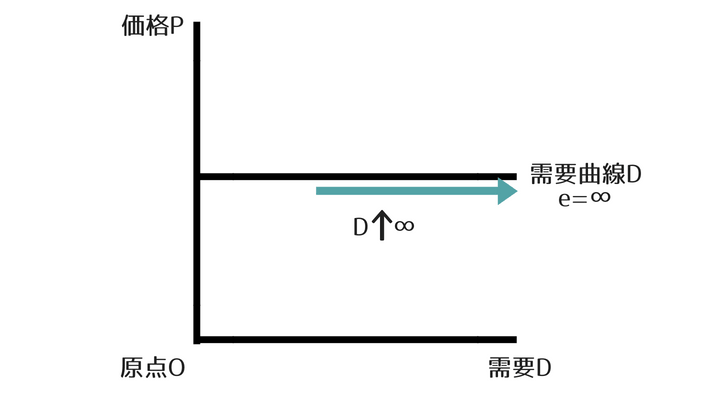
別のいい方をすると、需要の価格弾力性が無限大の場合、価格が少しでも低下すると、需要は無限に増加するため、もとの点と無限に増加した変化後の点を結ぶと需要曲線は水平になることになります。
需要の価格弾力性がゼロのケース:グラフは垂直
需要の価格弾力性がゼロ ⇒ 需要曲線は垂直になる
需要の価格弾力性がゼロというのは、小さいのが極端になったケースです。
極端に小さいというのは、マイナスではなくてゼロの場合ですので注意します。
需要の価格弾力性が小さい場合、需要曲線は急になるため、極端に急なら極端に急、つまり垂直になることになります。
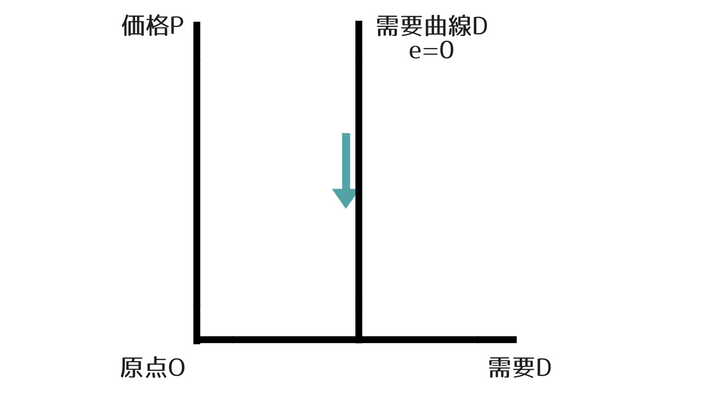
需要の価格弾力性がゼロの場合、価格が動いても需要は少しも変化しないことになります。
そのため、もとの点と変化後の点を結ぶと縦にまっすぐの線が描かれるため、需要曲線のグラフは垂直になることになります。
以上が、需要の価格弾力性と需要曲線のグラフの関係になります。
特殊な需要曲線と需要の価格弾力性の関係
特殊な需要曲線と需要の価格弾力性の関係として、需要曲線が右下がりの直線のケースと需要曲線が直角双曲線のケースを紹介します。
価格弾力性が変化するとき(直線の需要曲線)の需要曲線のグラフ
需要曲線が右下りの直線の場合、中点で需要の価格弾力性は1となります。
そして、グラフを右下に移動するにつれて需要の価格弾力性は小さくなり、グラフを左上に移動するにつれて需要の価格弾力性は大きくなります。
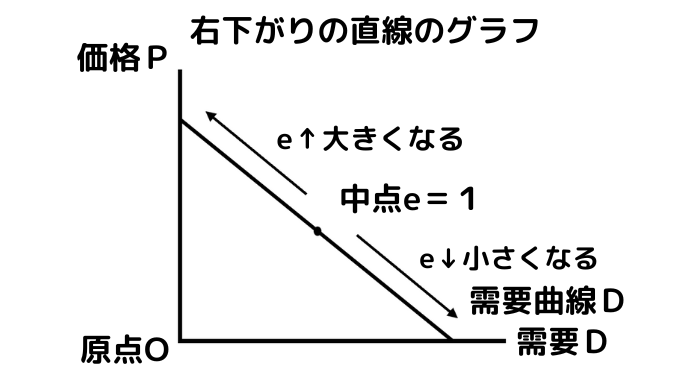
このように、需要曲線が右下りの直線の場合、需要の価格弾力性は点の移動に合わせて変化することになります。
価格弾力性が常に1のとき(直角双曲線)の需要曲線のグラフ
直角双曲線の需要の価格弾力性は常に1になります。
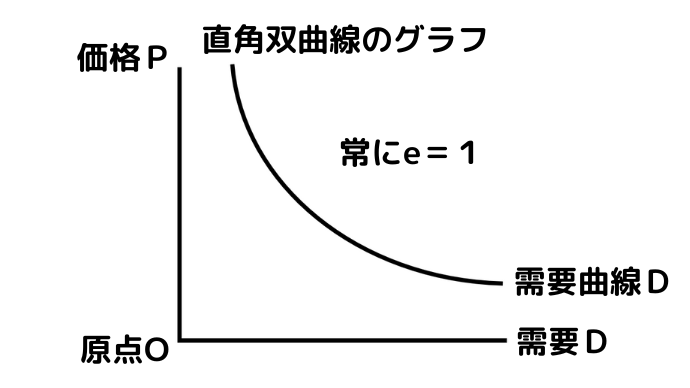
このように需要の価格弾力性が常に1のとき需要曲線のグラフは原点に対して出っ張った直角双曲線になります。